[문제]
가로의 길이가 N, 세로의 길이가 2인 직사각형 형태의 얇은 바닥이 있다. 태일이는 이 얇은 바닥을 1 X 2의 덮개,
2 X 1의 덮개, 2 X 2의 덮개를 이용해 채우고자 한다.
이때 바닥을 채우는 모든 경우의 수를 구하는 프로그램을 작성하시오.
예를 들어 2 X 3 크기의 바닥을 채우는 경우의 수는 5가지이다.
[입력 조건]
1. 첫째 줄에 N이 주어진다. (1 <= N <= 1,000)
[출력 조건]
첫째 줄에 2 X N 크기의 바닥을 채우는 방법의 수를 796,796으로 나눈 나머지를 출력한다.
<입력 예시>
3
<출력 예시>
5
[풀이]
# 정수 n을 입력받기
n = int(input())
# 앞서 계산된 결과를 저장하기 위한 DP 테이블 초기화
d = [0] * 1001
# 다이나믹 프로그래밍 진행
d[1] = 1
d[2] = 3
for i in range(3, n + 1) :
d[i] = (d[i-1] + 2 * d[i - 2]) % 796796
# 계산된 결과 출력
print(d[n])
1 X 2 크기의 바닥을 채우는 경우의 수는 1가지이며, 2 X 2 크기의 바닥을 채우는 경우의 수는 3이다.
또한, 왼쪽부터 i - 1까지 길이가 덮개로 이미 채워져 있으면 2 X 1의 덮개를 채우는 하나의 경우밖에 존재하지 않는다.

그리고 왼쪽부터 i -2까지 길이가 덮개로 이미 채워져 있으면 1 X 2 덮개 2개를 넣는 경우와 2 X 2의 덮개 하나를 넣는
경우로 2가지 경우가 존재한다. 참고로 2 X 1 덮개 2개를 넣는 경우를 고려하지 않는 이유는 위에서 이미 해당 경우가
고려되었기 때문이다.

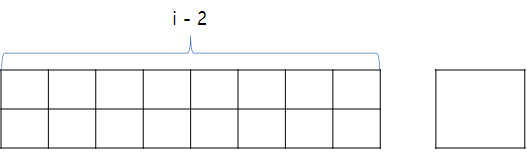
또한, i번째 위치에 대한 최적의 해를 구할 때 왼쪽부터 (i - 3)번째 이하의 위치에 대한 최적의 해에 대해서는
고려할 필요가 없다. 왜냐하면 사용할 수 있는 덮개의 형태가 최대 2 X 2 크기의 직사각형 형태이기 때문이다.
다시 말해 바닥을 채울 수 있는 형태는 위에서 언급한 경우밖에 없다. 따라서 다음과 같이 점화식을 세울 수 있다.
d[i] = d[i - 1] + d[i - 2] * 2
출처
이것이 코딩 테스트다 with 파이썬 - 나동빈 저
'알고리즘 > 이코테 실전문제' 카테고리의 다른 글
| [그래프 이론] 이코테 (파이썬) 도시 분할 계획 풀이 (0) | 2021.09.25 |
|---|---|
| [그래프 이론] 이코테 (파이썬) 팀 결성 풀이 (0) | 2021.09.25 |
| [최단 경로] 이코테 (파이썬) 전보 풀이 (0) | 2021.09.06 |
| [최단 경로] 이코테 (파이썬) 미래 도시 풀이 (0) | 2021.09.06 |
| [다이나믹 프로그래밍] 이코테 (파이썬) 병사 배치하기 풀이 (0) | 2021.08.30 |