이분 매칭은 집단이 존재할 때 A 집단이 B 집단을 선택하는 방법이다.
아래와 같이 숫자 집단과 알파벳 집단이 있다고 가정하고,

1번은 알파벳 A, B, C 를 선택하고 2번은 알파벳 A를, 3번은 알파벳 C를 선택했다고 할 때 이분 매칭은 모든 숫자가
각각의 알파벳을 선택하여 가장 많이 연결되는 경우를 탐색할 수 있도록 한다.
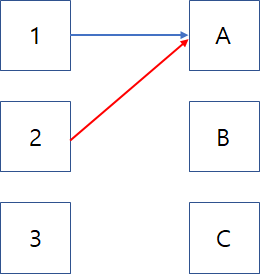
(1) 먼저 알파벳 A가 아무 번호에도 연결되어 있지 않기 때문에 1번이 알파벳 A를 선택한다.
(2) 2번이 A를 선택하는데 A는 1번에 연결되어 있기 때문에 A를 점유하고 있는 1번부터 다시 출발하여
A를 제외하고 다른 곳에 연결될 수 없는지 확인한다.
(3) 1번은 알파벳 B에 연결될 수 있기 때문에 B에 연결하고 2번은 A에 연결한다.
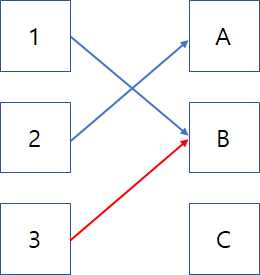
(4) 3번이 B를 선택하는데 B는 1번에 연결되어 있기 때문에 B를 점유하고 있는 1번부터 다시 출발하여
B를 제외하고 다른 곳에 연결될 수 없는지 확인한다.
(5) 알파벳 A는 이미 2번이 점유하고 있고, 알파벳 C는 비어있기 때문에 1번이 C에 연결하고 3번은 B에 연결한다.
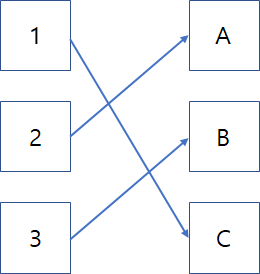
따라서, 최종적으로 위 그림과 같이 매칭될 수 있다.
[예제]
#include <iostream>
#include <vector>
#define MAX 101
using namespace std;
vector<int> a[MAX];
int d[MAX];
bool c[MAX];
int n=3, m;
bool dfs(int x) {
for(int i=0; i<a[x].size(); i++) {
int t = a[x][i];
if(c[t]) continue;
c[t] = true;
if(d[t] == 0 || dfs(d[t])) {
d[t] = x;
return true;
}
}
return false;
}
int main() {
a[1].push_back(1);
a[1].push_back(2);
a[1].push_back(3);
a[2].push_back(1);
a[3].push_back(2);
int count = 0;
for(int i=1; i<=n; i++) {
fill(c, c+MAX, false);
if(dfs(i)) count++;
}
printf("%d개의 매칭이 이루어짐\n", count);
for(int i=1; i<MAX; i++) {
if(d[i] != 0) {
printf("%d -> %d\n", d[i], i);
}
}
}
해당 소스코드는 C++로 작성한 코드이다.
메인 코드에서 위 그림 중 첫번째 그림과 같이 각 간선을 연결하고 그래프를 형성한 후, 첫번째 반복문에서 매번 매칭을
수행할 때마다 배열을 false 값으로 초기화해준다. 또한, 새롭게 매칭이 이루어지면 count 값을 1 증가시켜준다.
이분 매칭에 해당하는 dfs() 함수에서는 연결된 노드를 t 변수에 담아주고 만약 해당 노드가 이미 처리되어 true 값이라면
더 이상 볼 필요가 없기 때문에 넘어간다. 처리되지 않았다면 해당 노드를 true값으로 지정해준다.
그리고 만약 해당 노드가 비어있거나 점유 노드에 더 들어갈 공간이 있는 경우에는 매칭시켜 준 뒤 true값을 반환한다.
메인 코드의 마지막 반복문에서 어떻게 매칭이 이루어졌는지에 대한 정보를 출력한다.
[결과]

출처
https://blog.naver.com/ndb796/221240613074
29. 이분 매칭(Bipartite Matching)
지난 번에 네트워크 플로우(Network Flow) 알고리즘에 대해 공부하는 시간을 가졌습니다. 이번 시간에는 ...
blog.naver.com
'알고리즘 > 나동빈 실전 알고리즘' 카테고리의 다른 글
| 그리디 알고리즘(Greedy Algorithm) (0) | 2021.08.03 |
|---|---|
| 단순 비교 문자열 매칭 알고리즘 (0) | 2021.08.02 |
| 위상 정렬(Topology Sort) (0) | 2021.08.02 |
| 플로이드 와샬 알고리즘 (Floyd Warshall Algorithm) (0) | 2021.07.31 |
| 에라토스테네스의 체 (0) | 2021.07.28 |