Java으로 구현한 10844번 쉬운 계단 수 문제 풀이입니다.
https://www.acmicpc.net/problem/10844
10844번: 쉬운 계단 수
첫째 줄에 정답을 1,000,000,000으로 나눈 나머지를 출력한다.
www.acmicpc.net
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
public class Main {
static long mod = 1000000000;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(br.readLine());
long[][] dp = new long[n+1][10];
for (int i=1; i<10; i++)
dp[1][i] = 1;
for (int i=2; i<=n; i++) {
for (int j=0; j<10; j++) {
if (j == 0)
dp[i][j] = dp[i-1][j+1] % mod;
else if (j == 9)
dp[i][j] = dp[i-1][j-1] % mod;
else
dp[i][j] = (dp[i-1][j-1] + dp[i-1][j+1]) % mod;
}
}
long result = 0;
for (int i=0; i<10; i++)
result += dp[n][i];
System.out.println(result % mod);
}
}
1. 문제에서 요구되는 규칙을 따라 직접 표를 만들어 구성해보면 아래와 같다.
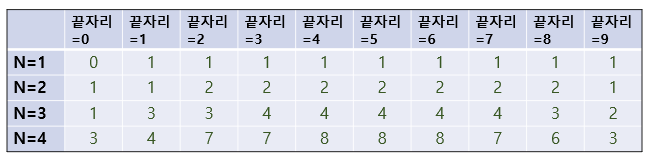
2. 위 표를 보면 N=1이면서 끝자리가 1-9인 경우 1가지씩 있으므로, 코드에서 첫번째 반복문으로 dp[1][i]를 1로 갱신한다.
3. 이중 for문을 통해 이후의 값들을 갱신해 나아가는데, 만약 j가 0일 경우 해당 위치에 dp[i-1][j+1] % 1000000000 을 할당한다.
4. 만약 j가 9일 경우 해당 위치에 dp[i-1][j-1] % 1000000000 을 할당한다.
5. 표를 보았을 때, 끝자리에 있는 수가 아닐 경우 특정 위치의 값은 대각선 왼쪽 위, 대각선 오른쪽 위의 합임을 알 수 있다.
6. 따라서 j가 0과 9 모두 아닐 경우 해당 위치에 dp[i-1][j-1] + dp[i-1][j+1] % 1000000000 을 연산하여 할당한다.
7. 반복문이 모두 끝난 후, 길이가 N인 계단 수의 총 갯수를 구해야하므로, dp[n]에 존재하는 모든 요소의 합을
1,000,000,000으로 나눈 나머지를 출력한다.
'백준(JAVA) 풀이 > 구현' 카테고리의 다른 글
| 백준(JAVA) 11057번 오르막 수 풀이 (0) | 2022.04.13 |
|---|---|
| 백준(JAVA) 11727번 2xn 타일링 2 풀이 (0) | 2022.04.07 |
| 백준(JAVA) 10992번 별 찍기 - 17 풀이 (0) | 2022.04.04 |
| 백준(JAVA) 10991번 별 찍기 - 16 풀이 (0) | 2022.04.04 |
| 백준(JAVA) 2446번 별 찍기 - 9 풀이 (0) | 2022.04.01 |