깊이 우선 탐색은 특정한 데이터를 탐색할 때 깊이를 우선으로 하여 탐색을 수행하는 탐색 알고리즘이다.
즉, 깊이 우선 탐색은 데이터를 보다 깊은 것을 우선으로 하여 탐색한다.
깊이 우선 탐색은 스택을 이용하는데, 컴퓨터는 구조적으로 항상 스택의 원리를 사용하기 때문에
스택을 사용하지 않고 단순히 재귀함수만을 사용해서도 구현이 가능하다.
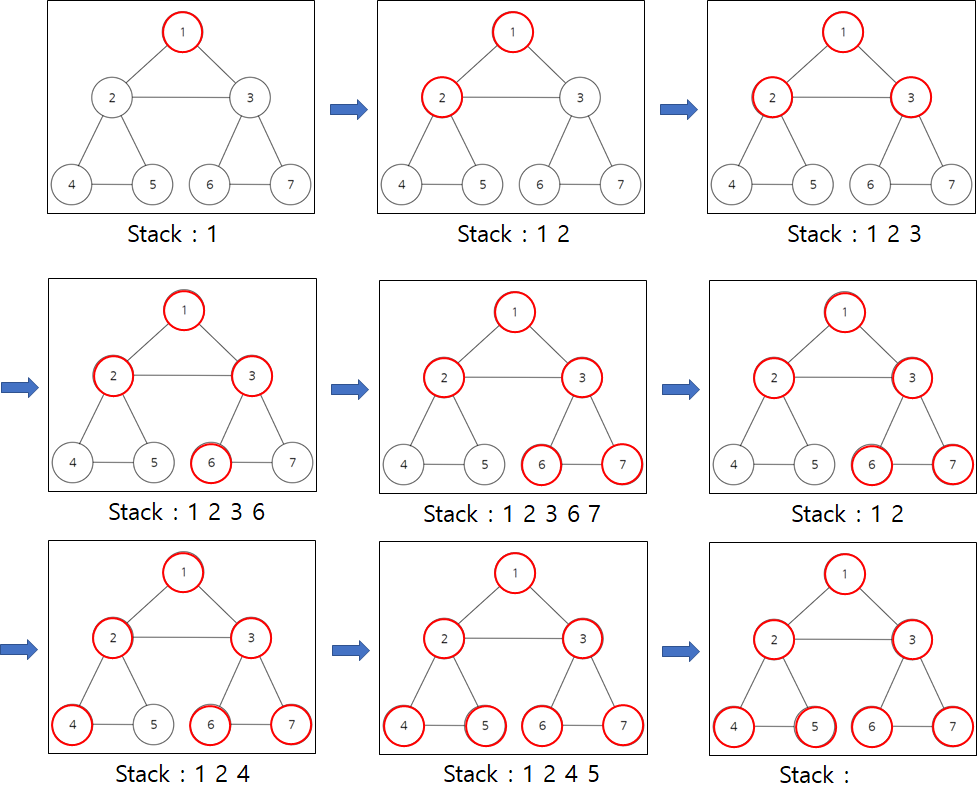
그림과 같이 스택의 최상단 노드를 확인하고 해당 노드와 인접한 노드 중 방문하지 않은 노드를 스택에 넣고
방문처리한다. 그림에 대해 구체적으로 설명하자면,
(1) 먼저 스택에 시작 노드인 1을 삽입하고 방문처리한다.
(2) 1과 인접한 노드 중 방문하지 않은 2를 스택에 삽입하고 방문처리한다.
(3) 2와 인접한 노드 중 방문하지 않은 3을 스택에 삽입하고 방문처리한다.
(4) 3와 인접한 노드 중 방문하지 않은 6을 스택에 삽입하고 방문처리한다.
(5) 6과 인접한 노드 중 방문하지 않은 7을 스택에 삽입하고 방문처리한다.
(6) 7과 인접한 노드 중 방문하지 않은 노드가 없기 때문에 7이 스택에서 빠져나온다.
(7) 방문하지 않은 노드가 없기 때문에 6, 3도 차례로 스택에서 빠져나온다.
(8) 2와 인접한 노드 중 방문하지 않은 4를 스택에 삽입하고 방문처리한다.
(9) 4와 인접한 노드 중 방문하지 않은 5를 스택에 삽입하고 방문처리한다.
(10) 방문하지 않은 노드가 없기 때문에 5, 4, 2, 1가 차례로 스택에서 빠져나온다.
==> 최종적으로 빈 스택을 확인할 수 있다. 방문 경로는 1 2 3 6 7 4 5 이다.
[예제]
#include <iostream>
#include <vector>
using namespace std;
int num = 7;
int c[8];
vector<int> a[8];
void dfs(int x) {
if(c[x]) return;
c[x] = true;
cout << x << ' ';
for(int i=0; i<a[x].size(); i++) {
int y = a[x][i];
dfs(y);
}
}
int main() {
a[1].push_back(2); //1과 2를 연결
a[2].push_back(1);
a[1].push_back(3); //1과 3을 연결
a[3].push_back(1);
a[2].push_back(3); //2와 3을 연결
a[3].push_back(2);
a[2].push_back(4); //2와 4를 연결
a[4].push_back(2);
a[2].push_back(5); //2와 5를 연결
a[5].push_back(2);
a[3].push_back(6); //3과 6을 연결
a[6].push_back(3);
a[3].push_back(7); //3과 7을 연결
a[7].push_back(3);
a[4].push_back(5); //4와 5를 연결
a[5].push_back(4);
a[6].push_back(7); //6과 7을 연결
a[7].push_back(6);
dfs(1); //시작점 1
}
해당 소스코드는 C++로 작성한 코드이며, 스택을 사용하지 않고 재귀함수만으로 코드를 구현하였다.
데이터를 저장하기 위해 vector 라이브러리를 정의해준 뒤, 생성한 dfs 함수 내에서 vector를 정의한다.
함수가 호출되면 특정한 x의 값을 받고 그 노드를 방문했다면 return을 통해 함수가 바로 끝나도록 하고
그 노드를 처음 방문하는 거라면 true를 넣어줌으로써 방문처리를 해주고 출력한다.
그리고 반복문을 통해 해당 노드와 인접한 노드들을 하나씩 방문하는데 그 인접 노드를 대상으로 dfs 함수를 수행하도록 한다.
메인코드에서는 각 노드의 정점을 연결해주고 dfs 함수 호출 시 시작점 데이터를 전송한다.
[결과]

출처
https://blog.naver.com/ndb796/221230945092
16. 깊이 우선 탐색(DFS)
깊이 우선 탐색(Depth First Search)은 탐색을 함에 있어서 보다 깊은 것을 우선적으로 하여 탐색하는 ...
blog.naver.com
'알고리즘 > 나동빈 실전 알고리즘' 카테고리의 다른 글
| 크루스칼 알고리즘(Kruskal Algorithm) (0) | 2021.07.22 |
|---|---|
| 합집합 찾기 알고리즘(Union-Find Algorithm) (0) | 2021.07.21 |
| 너비 우선 탐색(BFS; Breadth-first Search) (0) | 2021.07.21 |
| 큐(Queue) (0) | 2021.07.21 |
| 스택(Stack) (0) | 2021.07.21 |