힙정렬은 힙 트리 구조를 이용하는 정렬 방법이다.
여기서 힙 트리 구조는 최소값이나 최대값을 신속하게 찾아내기 위해 완전 이진 트리를 기반으로 하는 트리이다.
최대 힙은 부모노드가 자식노드보다 값이 큰 힙이다.

(1) 부모노드인 7이 자식노드인 5와 3보다 크다.
(2) 부모노드인 11이 자식노드인 9와 8보다 크다.
(3) 부모노드인 9가 자식노드인 7과 4보다 크다.
==> 그러므로 두 트리 모두 최대 힙이다.
[오름차순 정렬]
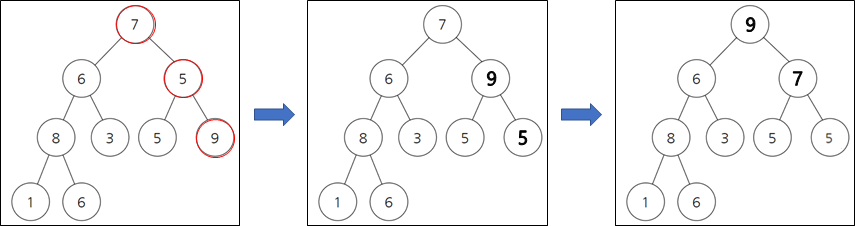

위 그림들은 오름차순 정렬을 수행하기에 앞서 최대 힙을 구성한 것입니다. 부모노드가 자식노드보다 작을 경우 값을
바꿔줌으로써 부모노드의 값이 더 크게 구성해줍니다.
이제 오름차순 정렬을 수행하는데 트리를 반으로 나눈 후 가장 최상위에 있는 루트노드 값을
가장 뒤쪽으로 보내면서 힙 트리의 크기를 1씩 감소해줍니다.

이러한 과정을 반복적으로 수행하면 최종적으로 오름차순으로 정렬된 트리를 확인할 수 있습니다.
[예제]
#include <stdio.h>
int num = 9;
int heap[9] = {7, 6, 5, 8, 3, 5, 9, 1, 6};
int main() {
for(int i=1; i<num; i++) {
int c = i;
do {
int root = (c-1) / 2; //특정한 원소의 부모
if(heap[root] < heap[c]) {
int temp = heap[root];
heap[root] = heap[c];
heap[c] = temp;
}
c = root;
} while (c != 0);
}
for(int i=num-1; i>=0; i--) {
int temp = heap[0];
heap[0] = heap[i];
heap[i] = temp;
int root = 0;
int c = 1;
do {
c = 2 * root + 1;
if(heap[c] < heap[c + 1] && c < i-1) {
c++;
}
if(heap[root] < heap[c] && c < i) {
int temp = heap[root];
heap[root] = heap[c];
heap[c] = temp;
}
root = c;
}while (c < i);
}
for(int i=0; i<num; i++) {
printf("%d ", heap[i]);
}
}
앞서 업로드한 그림과 같이 가장 먼저 최대 힙 구조를 구성한다. 특정한 원소의 부모를 구하고 부모노드가 자식노드보다
작을경우 자식 노드 값과 부모노드 값을 교체해주는 작업을 반복한다.
최대 힙 구조가 완료되면 오름차순 정렬을 위해 가장 큰 값을 맨 뒤로 보내준다. 그 후에 첫번째 반복문과 같이
다시 힙구조를 만들어주는 작업을 반복한다.
[결과]

[힙 정렬의 시간 복잡도]
힙 정렬의 전체 시간 복잡도는 O(N * logN) 이다.
힙 생성 알고리즘의 시간 복잡도는 한 번 자식노드로 내려갈 때마다 노드의 개수가 2배씩 증가한다는 점에서
O(logN) 이고 전체 데이터의 개수가 N개이기 때문에 O(N * logN)이라고 할 수 있다.
출처
https://blog.naver.com/ndb796/221228342808
10. 힙 정렬(Heap Sort)
힙 정렬(Heap Sort)은 병합 정렬(Merge Sort)와 퀵 정렬(Quick Sort)만큼 빠른 정렬 알고리즘입니다....
blog.naver.com
'알고리즘 > 나동빈 실전 알고리즘' 카테고리의 다른 글
| 스택(Stack) (0) | 2021.07.21 |
|---|---|
| 계수 정렬(Counting Sort) (0) | 2021.07.20 |
| 병합정렬(Merge Sort) (0) | 2021.07.20 |
| 퀵정렬(Quick Sort) (0) | 2021.07.16 |
| 삽입정렬(Insertion Sort) (0) | 2021.07.16 |